Why looks the Moire pattern on my screen like the contour plot of z = xy?
I am not completely sure, but the Moiré pattern on photo's of my screen looks suspiciously like a contour plot of z = xy.
I couldn't find any reference or similar question. Is there a fundamental reason for this, or does it seem to be merely a coincidence?
Moiré pattern on my screen:

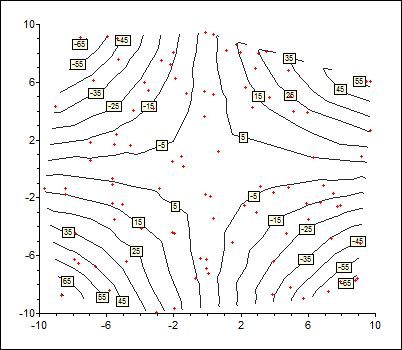
Contour plot of z = xy:
graphing-functions
add a comment |
I am not completely sure, but the Moiré pattern on photo's of my screen looks suspiciously like a contour plot of z = xy.
I couldn't find any reference or similar question. Is there a fundamental reason for this, or does it seem to be merely a coincidence?
Moiré pattern on my screen:

Contour plot of z = xy:

graphing-functions
Maybe it is because of how the phone's camera is composed.
– manooooh
Dec 28 '18 at 19:10
what type (technology) of screen is it ?
– G Cab
Dec 29 '18 at 17:48
3
xkcd.com/1814 Still cracks me up every time I read it.
– heropup
Dec 30 '18 at 5:52
add a comment |
I am not completely sure, but the Moiré pattern on photo's of my screen looks suspiciously like a contour plot of z = xy.
I couldn't find any reference or similar question. Is there a fundamental reason for this, or does it seem to be merely a coincidence?
Moiré pattern on my screen:

Contour plot of z = xy:

graphing-functions
I am not completely sure, but the Moiré pattern on photo's of my screen looks suspiciously like a contour plot of z = xy.
I couldn't find any reference or similar question. Is there a fundamental reason for this, or does it seem to be merely a coincidence?
Moiré pattern on my screen:

Contour plot of z = xy:

graphing-functions
graphing-functions
asked Dec 28 '18 at 19:08
Ruben
496212
496212
Maybe it is because of how the phone's camera is composed.
– manooooh
Dec 28 '18 at 19:10
what type (technology) of screen is it ?
– G Cab
Dec 29 '18 at 17:48
3
xkcd.com/1814 Still cracks me up every time I read it.
– heropup
Dec 30 '18 at 5:52
add a comment |
Maybe it is because of how the phone's camera is composed.
– manooooh
Dec 28 '18 at 19:10
what type (technology) of screen is it ?
– G Cab
Dec 29 '18 at 17:48
3
xkcd.com/1814 Still cracks me up every time I read it.
– heropup
Dec 30 '18 at 5:52
Maybe it is because of how the phone's camera is composed.
– manooooh
Dec 28 '18 at 19:10
Maybe it is because of how the phone's camera is composed.
– manooooh
Dec 28 '18 at 19:10
what type (technology) of screen is it ?
– G Cab
Dec 29 '18 at 17:48
what type (technology) of screen is it ?
– G Cab
Dec 29 '18 at 17:48
3
3
xkcd.com/1814 Still cracks me up every time I read it.
– heropup
Dec 30 '18 at 5:52
xkcd.com/1814 Still cracks me up every time I read it.
– heropup
Dec 30 '18 at 5:52
add a comment |
2 Answers
2
active
oldest
votes
The reason is due to slight mismatch of two coordinate systems. For a simple example, suppose we have the usual Cartesian coordinate system and another affine coordinate systems which is slightly off. That is, the points with coordinates $(0,0), (1,0), (0,1)$ are mapped to the same points but the point with coordinates $(1,1)$ is mapped to the point $(1+t,1+t)$ where $t$ is small. But now, the point with coordinates $(x,y)$ is mapped to the point $(x+xyt,y+xyt)$. The point with coordinates $(x,y$) is mapped to $(a+bx+cy+dxy,e+fx+gy+hxy)$
in the most general affine mapping and even more complicated in a general projective mapping, but I deliberately chose a very simple case.
The difference in coordinates is $(xyt,xyt)$. If we assume that $xyt$ is a small fixed quantity based on screen resolution, then $x$ and $y$ are inversely proportional which explains the similarity to a $z=xy$ contour plot.
The photo taken was slightly tilted and not strictly parallel to the plane of the screen. The actual situation here is more complicated due to real world effects such as projective mappings than the simple example I gave, but it essentially has similar features and similar moire effects. This is no "physical effect" but a mathematical and geometrical one as I will now demonstrate.
I tested this effect with some Wolfram Mathematica code:
wc[p1_, w1_, p2_, w2_] := (p1*w1 + p2*w2)/(w1 + w2);
VGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L1[[2]], n - i],
wc[L2[[1]], i, L2[[2]], n - i]}], {i, 0, n}];
HGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L2[[1]], n - i],
wc[L1[[2]], i, L2[[2]], n - i]}], {i, 0, n}];
HVGrid[L1_, L2_, n_: 1, m_: 1] :=
Join[VGrid[L1, L2, n], HGrid[L1, L2, m]];
With[{M=60, p1={0, 0}, p2={1, 0}, p3={0, 1}, p4={1, 1}},
Graphics[Join[HVGrid[{p1, p2}, {p3, p4}, M, M],
HVGrid[{p1, p2}, {p3, p4 (1-9/M)}, M, M]], ImageSize->300]]
You can try it yourself at Wolfram Development Platform by creating a new notebook.
The Moire pattern image with $t=-9/60$ is this:

You can see the resemblance to the top right quarter of
the screen shot.
5
It's not really clear to me where you get $(x+xyt,y+xyt)$ here. It seems to be pulled out of a hat to match the effect you're ostensibly explaining. Which "physical" effect would lead to that kind of mapping?
– Henning Makholm
Dec 29 '18 at 15:45
I think that a bilinear transform is less natural than a projective transform which would be here, to be in good matching with your own transform : $X(x,y)=(ax/(x+y+a-1)),Y(x,y)=(ay/(x+y+a-1))$ with $a=5$ or so...
– Jean Marie
Dec 30 '18 at 23:52
@JeanMarie Thank you for mentioning projective transform. The whole idea behind projective geometry was to deal with creating flat images of 3D scenes with proper "perspective". I agree it would be more a bit more natural and accurate to take perspective into account, but I decided here it would be more practical and better to go for simplicity instead.
– Somos
Dec 31 '18 at 4:35
add a comment |
Interference occurs when there are two rectangular grids.. One sees the phenomenon in window curtains, green house and fishing nets thin textiles &c. The grid lines can be either continuous or discrete with dots.
A screenshot of computer screen on a mobile camera I could observe several Moiré fringes similar the one in question depending on relative orientations of cameras and their relative out-of-flatness, we need to zoom a couple of times Control+.

Without going much into geometric quantitative Physics detail the Moire fringe locus is in principle the same as Newton's Ring locus for a coarser wavelength/grid size scale.
Due to the path length difference in Moire Fringes & Newton's Rings both have formation of fringes typical of 1) elliptic 2) saddle 3) flat relative level topographies.
The fringes also reflect Dupin's indicatrices in differential geometry revealing positive, negative and zero Gauss curvatures.They give rise to a family of ellipses/hyperbolae/straight lines respectively.
A path difference of the given image is produced when One of the transparent reticulated plate/dot junction grids ( in optics .. zone plates) are closest/farthest along NorthEast-SouthWest directions compared to NorthWest-SouthEast direction for constant $ z= xy$ fringes. When the plates are carefully rotated by $ 45^{circ},$ the high features shift to NorthSouth-EastWest for constant $z= x^2-y^2$ fringes.
How does any of this have to do with a digial screen shot taken by a digital camera? There are no "zone plates" involved here. There was no "carefully rotated ty $45^{circ}$".
– Somos
Dec 30 '18 at 1:05
Interference is possible when there are two rectangular grids.. one is a raster of tiny pixels on the screen and the other is a raster of the camera screen. I have also obtained the same image. You can also obtain it. Shall upload it later and find the suitable conditions for a snap.
– Narasimham
Dec 30 '18 at 4:46
@Somos Small rotation ok, not necessary through $ 45^∘ $
– Narasimham
yesterday
add a comment |
Your Answer
StackExchange.ifUsing("editor", function () {
return StackExchange.using("mathjaxEditing", function () {
StackExchange.MarkdownEditor.creationCallbacks.add(function (editor, postfix) {
StackExchange.mathjaxEditing.prepareWmdForMathJax(editor, postfix, [["$", "$"], ["\\(","\\)"]]);
});
});
}, "mathjax-editing");
StackExchange.ready(function() {
var channelOptions = {
tags: "".split(" "),
id: "69"
};
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function() {
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled) {
StackExchange.using("snippets", function() {
createEditor();
});
}
else {
createEditor();
}
});
function createEditor() {
StackExchange.prepareEditor({
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader: {
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
},
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
});
}
});
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f3055202%2fwhy-looks-the-moire-pattern-on-my-screen-like-the-contour-plot-of-z-xy%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
2 Answers
2
active
oldest
votes
2 Answers
2
active
oldest
votes
active
oldest
votes
active
oldest
votes
The reason is due to slight mismatch of two coordinate systems. For a simple example, suppose we have the usual Cartesian coordinate system and another affine coordinate systems which is slightly off. That is, the points with coordinates $(0,0), (1,0), (0,1)$ are mapped to the same points but the point with coordinates $(1,1)$ is mapped to the point $(1+t,1+t)$ where $t$ is small. But now, the point with coordinates $(x,y)$ is mapped to the point $(x+xyt,y+xyt)$. The point with coordinates $(x,y$) is mapped to $(a+bx+cy+dxy,e+fx+gy+hxy)$
in the most general affine mapping and even more complicated in a general projective mapping, but I deliberately chose a very simple case.
The difference in coordinates is $(xyt,xyt)$. If we assume that $xyt$ is a small fixed quantity based on screen resolution, then $x$ and $y$ are inversely proportional which explains the similarity to a $z=xy$ contour plot.
The photo taken was slightly tilted and not strictly parallel to the plane of the screen. The actual situation here is more complicated due to real world effects such as projective mappings than the simple example I gave, but it essentially has similar features and similar moire effects. This is no "physical effect" but a mathematical and geometrical one as I will now demonstrate.
I tested this effect with some Wolfram Mathematica code:
wc[p1_, w1_, p2_, w2_] := (p1*w1 + p2*w2)/(w1 + w2);
VGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L1[[2]], n - i],
wc[L2[[1]], i, L2[[2]], n - i]}], {i, 0, n}];
HGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L2[[1]], n - i],
wc[L1[[2]], i, L2[[2]], n - i]}], {i, 0, n}];
HVGrid[L1_, L2_, n_: 1, m_: 1] :=
Join[VGrid[L1, L2, n], HGrid[L1, L2, m]];
With[{M=60, p1={0, 0}, p2={1, 0}, p3={0, 1}, p4={1, 1}},
Graphics[Join[HVGrid[{p1, p2}, {p3, p4}, M, M],
HVGrid[{p1, p2}, {p3, p4 (1-9/M)}, M, M]], ImageSize->300]]
You can try it yourself at Wolfram Development Platform by creating a new notebook.
The Moire pattern image with $t=-9/60$ is this:

You can see the resemblance to the top right quarter of
the screen shot.
5
It's not really clear to me where you get $(x+xyt,y+xyt)$ here. It seems to be pulled out of a hat to match the effect you're ostensibly explaining. Which "physical" effect would lead to that kind of mapping?
– Henning Makholm
Dec 29 '18 at 15:45
I think that a bilinear transform is less natural than a projective transform which would be here, to be in good matching with your own transform : $X(x,y)=(ax/(x+y+a-1)),Y(x,y)=(ay/(x+y+a-1))$ with $a=5$ or so...
– Jean Marie
Dec 30 '18 at 23:52
@JeanMarie Thank you for mentioning projective transform. The whole idea behind projective geometry was to deal with creating flat images of 3D scenes with proper "perspective". I agree it would be more a bit more natural and accurate to take perspective into account, but I decided here it would be more practical and better to go for simplicity instead.
– Somos
Dec 31 '18 at 4:35
add a comment |
The reason is due to slight mismatch of two coordinate systems. For a simple example, suppose we have the usual Cartesian coordinate system and another affine coordinate systems which is slightly off. That is, the points with coordinates $(0,0), (1,0), (0,1)$ are mapped to the same points but the point with coordinates $(1,1)$ is mapped to the point $(1+t,1+t)$ where $t$ is small. But now, the point with coordinates $(x,y)$ is mapped to the point $(x+xyt,y+xyt)$. The point with coordinates $(x,y$) is mapped to $(a+bx+cy+dxy,e+fx+gy+hxy)$
in the most general affine mapping and even more complicated in a general projective mapping, but I deliberately chose a very simple case.
The difference in coordinates is $(xyt,xyt)$. If we assume that $xyt$ is a small fixed quantity based on screen resolution, then $x$ and $y$ are inversely proportional which explains the similarity to a $z=xy$ contour plot.
The photo taken was slightly tilted and not strictly parallel to the plane of the screen. The actual situation here is more complicated due to real world effects such as projective mappings than the simple example I gave, but it essentially has similar features and similar moire effects. This is no "physical effect" but a mathematical and geometrical one as I will now demonstrate.
I tested this effect with some Wolfram Mathematica code:
wc[p1_, w1_, p2_, w2_] := (p1*w1 + p2*w2)/(w1 + w2);
VGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L1[[2]], n - i],
wc[L2[[1]], i, L2[[2]], n - i]}], {i, 0, n}];
HGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L2[[1]], n - i],
wc[L1[[2]], i, L2[[2]], n - i]}], {i, 0, n}];
HVGrid[L1_, L2_, n_: 1, m_: 1] :=
Join[VGrid[L1, L2, n], HGrid[L1, L2, m]];
With[{M=60, p1={0, 0}, p2={1, 0}, p3={0, 1}, p4={1, 1}},
Graphics[Join[HVGrid[{p1, p2}, {p3, p4}, M, M],
HVGrid[{p1, p2}, {p3, p4 (1-9/M)}, M, M]], ImageSize->300]]
You can try it yourself at Wolfram Development Platform by creating a new notebook.
The Moire pattern image with $t=-9/60$ is this:

You can see the resemblance to the top right quarter of
the screen shot.
5
It's not really clear to me where you get $(x+xyt,y+xyt)$ here. It seems to be pulled out of a hat to match the effect you're ostensibly explaining. Which "physical" effect would lead to that kind of mapping?
– Henning Makholm
Dec 29 '18 at 15:45
I think that a bilinear transform is less natural than a projective transform which would be here, to be in good matching with your own transform : $X(x,y)=(ax/(x+y+a-1)),Y(x,y)=(ay/(x+y+a-1))$ with $a=5$ or so...
– Jean Marie
Dec 30 '18 at 23:52
@JeanMarie Thank you for mentioning projective transform. The whole idea behind projective geometry was to deal with creating flat images of 3D scenes with proper "perspective". I agree it would be more a bit more natural and accurate to take perspective into account, but I decided here it would be more practical and better to go for simplicity instead.
– Somos
Dec 31 '18 at 4:35
add a comment |
The reason is due to slight mismatch of two coordinate systems. For a simple example, suppose we have the usual Cartesian coordinate system and another affine coordinate systems which is slightly off. That is, the points with coordinates $(0,0), (1,0), (0,1)$ are mapped to the same points but the point with coordinates $(1,1)$ is mapped to the point $(1+t,1+t)$ where $t$ is small. But now, the point with coordinates $(x,y)$ is mapped to the point $(x+xyt,y+xyt)$. The point with coordinates $(x,y$) is mapped to $(a+bx+cy+dxy,e+fx+gy+hxy)$
in the most general affine mapping and even more complicated in a general projective mapping, but I deliberately chose a very simple case.
The difference in coordinates is $(xyt,xyt)$. If we assume that $xyt$ is a small fixed quantity based on screen resolution, then $x$ and $y$ are inversely proportional which explains the similarity to a $z=xy$ contour plot.
The photo taken was slightly tilted and not strictly parallel to the plane of the screen. The actual situation here is more complicated due to real world effects such as projective mappings than the simple example I gave, but it essentially has similar features and similar moire effects. This is no "physical effect" but a mathematical and geometrical one as I will now demonstrate.
I tested this effect with some Wolfram Mathematica code:
wc[p1_, w1_, p2_, w2_] := (p1*w1 + p2*w2)/(w1 + w2);
VGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L1[[2]], n - i],
wc[L2[[1]], i, L2[[2]], n - i]}], {i, 0, n}];
HGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L2[[1]], n - i],
wc[L1[[2]], i, L2[[2]], n - i]}], {i, 0, n}];
HVGrid[L1_, L2_, n_: 1, m_: 1] :=
Join[VGrid[L1, L2, n], HGrid[L1, L2, m]];
With[{M=60, p1={0, 0}, p2={1, 0}, p3={0, 1}, p4={1, 1}},
Graphics[Join[HVGrid[{p1, p2}, {p3, p4}, M, M],
HVGrid[{p1, p2}, {p3, p4 (1-9/M)}, M, M]], ImageSize->300]]
You can try it yourself at Wolfram Development Platform by creating a new notebook.
The Moire pattern image with $t=-9/60$ is this:

You can see the resemblance to the top right quarter of
the screen shot.
The reason is due to slight mismatch of two coordinate systems. For a simple example, suppose we have the usual Cartesian coordinate system and another affine coordinate systems which is slightly off. That is, the points with coordinates $(0,0), (1,0), (0,1)$ are mapped to the same points but the point with coordinates $(1,1)$ is mapped to the point $(1+t,1+t)$ where $t$ is small. But now, the point with coordinates $(x,y)$ is mapped to the point $(x+xyt,y+xyt)$. The point with coordinates $(x,y$) is mapped to $(a+bx+cy+dxy,e+fx+gy+hxy)$
in the most general affine mapping and even more complicated in a general projective mapping, but I deliberately chose a very simple case.
The difference in coordinates is $(xyt,xyt)$. If we assume that $xyt$ is a small fixed quantity based on screen resolution, then $x$ and $y$ are inversely proportional which explains the similarity to a $z=xy$ contour plot.
The photo taken was slightly tilted and not strictly parallel to the plane of the screen. The actual situation here is more complicated due to real world effects such as projective mappings than the simple example I gave, but it essentially has similar features and similar moire effects. This is no "physical effect" but a mathematical and geometrical one as I will now demonstrate.
I tested this effect with some Wolfram Mathematica code:
wc[p1_, w1_, p2_, w2_] := (p1*w1 + p2*w2)/(w1 + w2);
VGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L1[[2]], n - i],
wc[L2[[1]], i, L2[[2]], n - i]}], {i, 0, n}];
HGrid[L1_, L2_, n_: 1] :=
Table[Line[{wc[L1[[1]], i, L2[[1]], n - i],
wc[L1[[2]], i, L2[[2]], n - i]}], {i, 0, n}];
HVGrid[L1_, L2_, n_: 1, m_: 1] :=
Join[VGrid[L1, L2, n], HGrid[L1, L2, m]];
With[{M=60, p1={0, 0}, p2={1, 0}, p3={0, 1}, p4={1, 1}},
Graphics[Join[HVGrid[{p1, p2}, {p3, p4}, M, M],
HVGrid[{p1, p2}, {p3, p4 (1-9/M)}, M, M]], ImageSize->300]]
You can try it yourself at Wolfram Development Platform by creating a new notebook.
The Moire pattern image with $t=-9/60$ is this:

You can see the resemblance to the top right quarter of
the screen shot.
edited Dec 31 '18 at 4:40
answered Dec 29 '18 at 1:24
Somos
13.1k11034
13.1k11034
5
It's not really clear to me where you get $(x+xyt,y+xyt)$ here. It seems to be pulled out of a hat to match the effect you're ostensibly explaining. Which "physical" effect would lead to that kind of mapping?
– Henning Makholm
Dec 29 '18 at 15:45
I think that a bilinear transform is less natural than a projective transform which would be here, to be in good matching with your own transform : $X(x,y)=(ax/(x+y+a-1)),Y(x,y)=(ay/(x+y+a-1))$ with $a=5$ or so...
– Jean Marie
Dec 30 '18 at 23:52
@JeanMarie Thank you for mentioning projective transform. The whole idea behind projective geometry was to deal with creating flat images of 3D scenes with proper "perspective". I agree it would be more a bit more natural and accurate to take perspective into account, but I decided here it would be more practical and better to go for simplicity instead.
– Somos
Dec 31 '18 at 4:35
add a comment |
5
It's not really clear to me where you get $(x+xyt,y+xyt)$ here. It seems to be pulled out of a hat to match the effect you're ostensibly explaining. Which "physical" effect would lead to that kind of mapping?
– Henning Makholm
Dec 29 '18 at 15:45
I think that a bilinear transform is less natural than a projective transform which would be here, to be in good matching with your own transform : $X(x,y)=(ax/(x+y+a-1)),Y(x,y)=(ay/(x+y+a-1))$ with $a=5$ or so...
– Jean Marie
Dec 30 '18 at 23:52
@JeanMarie Thank you for mentioning projective transform. The whole idea behind projective geometry was to deal with creating flat images of 3D scenes with proper "perspective". I agree it would be more a bit more natural and accurate to take perspective into account, but I decided here it would be more practical and better to go for simplicity instead.
– Somos
Dec 31 '18 at 4:35
5
5
It's not really clear to me where you get $(x+xyt,y+xyt)$ here. It seems to be pulled out of a hat to match the effect you're ostensibly explaining. Which "physical" effect would lead to that kind of mapping?
– Henning Makholm
Dec 29 '18 at 15:45
It's not really clear to me where you get $(x+xyt,y+xyt)$ here. It seems to be pulled out of a hat to match the effect you're ostensibly explaining. Which "physical" effect would lead to that kind of mapping?
– Henning Makholm
Dec 29 '18 at 15:45
I think that a bilinear transform is less natural than a projective transform which would be here, to be in good matching with your own transform : $X(x,y)=(ax/(x+y+a-1)),Y(x,y)=(ay/(x+y+a-1))$ with $a=5$ or so...
– Jean Marie
Dec 30 '18 at 23:52
I think that a bilinear transform is less natural than a projective transform which would be here, to be in good matching with your own transform : $X(x,y)=(ax/(x+y+a-1)),Y(x,y)=(ay/(x+y+a-1))$ with $a=5$ or so...
– Jean Marie
Dec 30 '18 at 23:52
@JeanMarie Thank you for mentioning projective transform. The whole idea behind projective geometry was to deal with creating flat images of 3D scenes with proper "perspective". I agree it would be more a bit more natural and accurate to take perspective into account, but I decided here it would be more practical and better to go for simplicity instead.
– Somos
Dec 31 '18 at 4:35
@JeanMarie Thank you for mentioning projective transform. The whole idea behind projective geometry was to deal with creating flat images of 3D scenes with proper "perspective". I agree it would be more a bit more natural and accurate to take perspective into account, but I decided here it would be more practical and better to go for simplicity instead.
– Somos
Dec 31 '18 at 4:35
add a comment |
Interference occurs when there are two rectangular grids.. One sees the phenomenon in window curtains, green house and fishing nets thin textiles &c. The grid lines can be either continuous or discrete with dots.
A screenshot of computer screen on a mobile camera I could observe several Moiré fringes similar the one in question depending on relative orientations of cameras and their relative out-of-flatness, we need to zoom a couple of times Control+.

Without going much into geometric quantitative Physics detail the Moire fringe locus is in principle the same as Newton's Ring locus for a coarser wavelength/grid size scale.
Due to the path length difference in Moire Fringes & Newton's Rings both have formation of fringes typical of 1) elliptic 2) saddle 3) flat relative level topographies.
The fringes also reflect Dupin's indicatrices in differential geometry revealing positive, negative and zero Gauss curvatures.They give rise to a family of ellipses/hyperbolae/straight lines respectively.
A path difference of the given image is produced when One of the transparent reticulated plate/dot junction grids ( in optics .. zone plates) are closest/farthest along NorthEast-SouthWest directions compared to NorthWest-SouthEast direction for constant $ z= xy$ fringes. When the plates are carefully rotated by $ 45^{circ},$ the high features shift to NorthSouth-EastWest for constant $z= x^2-y^2$ fringes.
How does any of this have to do with a digial screen shot taken by a digital camera? There are no "zone plates" involved here. There was no "carefully rotated ty $45^{circ}$".
– Somos
Dec 30 '18 at 1:05
Interference is possible when there are two rectangular grids.. one is a raster of tiny pixels on the screen and the other is a raster of the camera screen. I have also obtained the same image. You can also obtain it. Shall upload it later and find the suitable conditions for a snap.
– Narasimham
Dec 30 '18 at 4:46
@Somos Small rotation ok, not necessary through $ 45^∘ $
– Narasimham
yesterday
add a comment |
Interference occurs when there are two rectangular grids.. One sees the phenomenon in window curtains, green house and fishing nets thin textiles &c. The grid lines can be either continuous or discrete with dots.
A screenshot of computer screen on a mobile camera I could observe several Moiré fringes similar the one in question depending on relative orientations of cameras and their relative out-of-flatness, we need to zoom a couple of times Control+.

Without going much into geometric quantitative Physics detail the Moire fringe locus is in principle the same as Newton's Ring locus for a coarser wavelength/grid size scale.
Due to the path length difference in Moire Fringes & Newton's Rings both have formation of fringes typical of 1) elliptic 2) saddle 3) flat relative level topographies.
The fringes also reflect Dupin's indicatrices in differential geometry revealing positive, negative and zero Gauss curvatures.They give rise to a family of ellipses/hyperbolae/straight lines respectively.
A path difference of the given image is produced when One of the transparent reticulated plate/dot junction grids ( in optics .. zone plates) are closest/farthest along NorthEast-SouthWest directions compared to NorthWest-SouthEast direction for constant $ z= xy$ fringes. When the plates are carefully rotated by $ 45^{circ},$ the high features shift to NorthSouth-EastWest for constant $z= x^2-y^2$ fringes.
How does any of this have to do with a digial screen shot taken by a digital camera? There are no "zone plates" involved here. There was no "carefully rotated ty $45^{circ}$".
– Somos
Dec 30 '18 at 1:05
Interference is possible when there are two rectangular grids.. one is a raster of tiny pixels on the screen and the other is a raster of the camera screen. I have also obtained the same image. You can also obtain it. Shall upload it later and find the suitable conditions for a snap.
– Narasimham
Dec 30 '18 at 4:46
@Somos Small rotation ok, not necessary through $ 45^∘ $
– Narasimham
yesterday
add a comment |
Interference occurs when there are two rectangular grids.. One sees the phenomenon in window curtains, green house and fishing nets thin textiles &c. The grid lines can be either continuous or discrete with dots.
A screenshot of computer screen on a mobile camera I could observe several Moiré fringes similar the one in question depending on relative orientations of cameras and their relative out-of-flatness, we need to zoom a couple of times Control+.

Without going much into geometric quantitative Physics detail the Moire fringe locus is in principle the same as Newton's Ring locus for a coarser wavelength/grid size scale.
Due to the path length difference in Moire Fringes & Newton's Rings both have formation of fringes typical of 1) elliptic 2) saddle 3) flat relative level topographies.
The fringes also reflect Dupin's indicatrices in differential geometry revealing positive, negative and zero Gauss curvatures.They give rise to a family of ellipses/hyperbolae/straight lines respectively.
A path difference of the given image is produced when One of the transparent reticulated plate/dot junction grids ( in optics .. zone plates) are closest/farthest along NorthEast-SouthWest directions compared to NorthWest-SouthEast direction for constant $ z= xy$ fringes. When the plates are carefully rotated by $ 45^{circ},$ the high features shift to NorthSouth-EastWest for constant $z= x^2-y^2$ fringes.
Interference occurs when there are two rectangular grids.. One sees the phenomenon in window curtains, green house and fishing nets thin textiles &c. The grid lines can be either continuous or discrete with dots.
A screenshot of computer screen on a mobile camera I could observe several Moiré fringes similar the one in question depending on relative orientations of cameras and their relative out-of-flatness, we need to zoom a couple of times Control+.

Without going much into geometric quantitative Physics detail the Moire fringe locus is in principle the same as Newton's Ring locus for a coarser wavelength/grid size scale.
Due to the path length difference in Moire Fringes & Newton's Rings both have formation of fringes typical of 1) elliptic 2) saddle 3) flat relative level topographies.
The fringes also reflect Dupin's indicatrices in differential geometry revealing positive, negative and zero Gauss curvatures.They give rise to a family of ellipses/hyperbolae/straight lines respectively.
A path difference of the given image is produced when One of the transparent reticulated plate/dot junction grids ( in optics .. zone plates) are closest/farthest along NorthEast-SouthWest directions compared to NorthWest-SouthEast direction for constant $ z= xy$ fringes. When the plates are carefully rotated by $ 45^{circ},$ the high features shift to NorthSouth-EastWest for constant $z= x^2-y^2$ fringes.
edited yesterday
answered Dec 29 '18 at 19:49
Narasimham
20.6k52158
20.6k52158
How does any of this have to do with a digial screen shot taken by a digital camera? There are no "zone plates" involved here. There was no "carefully rotated ty $45^{circ}$".
– Somos
Dec 30 '18 at 1:05
Interference is possible when there are two rectangular grids.. one is a raster of tiny pixels on the screen and the other is a raster of the camera screen. I have also obtained the same image. You can also obtain it. Shall upload it later and find the suitable conditions for a snap.
– Narasimham
Dec 30 '18 at 4:46
@Somos Small rotation ok, not necessary through $ 45^∘ $
– Narasimham
yesterday
add a comment |
How does any of this have to do with a digial screen shot taken by a digital camera? There are no "zone plates" involved here. There was no "carefully rotated ty $45^{circ}$".
– Somos
Dec 30 '18 at 1:05
Interference is possible when there are two rectangular grids.. one is a raster of tiny pixels on the screen and the other is a raster of the camera screen. I have also obtained the same image. You can also obtain it. Shall upload it later and find the suitable conditions for a snap.
– Narasimham
Dec 30 '18 at 4:46
@Somos Small rotation ok, not necessary through $ 45^∘ $
– Narasimham
yesterday
How does any of this have to do with a digial screen shot taken by a digital camera? There are no "zone plates" involved here. There was no "carefully rotated ty $45^{circ}$".
– Somos
Dec 30 '18 at 1:05
How does any of this have to do with a digial screen shot taken by a digital camera? There are no "zone plates" involved here. There was no "carefully rotated ty $45^{circ}$".
– Somos
Dec 30 '18 at 1:05
Interference is possible when there are two rectangular grids.. one is a raster of tiny pixels on the screen and the other is a raster of the camera screen. I have also obtained the same image. You can also obtain it. Shall upload it later and find the suitable conditions for a snap.
– Narasimham
Dec 30 '18 at 4:46
Interference is possible when there are two rectangular grids.. one is a raster of tiny pixels on the screen and the other is a raster of the camera screen. I have also obtained the same image. You can also obtain it. Shall upload it later and find the suitable conditions for a snap.
– Narasimham
Dec 30 '18 at 4:46
@Somos Small rotation ok, not necessary through $ 45^∘ $
– Narasimham
yesterday
@Somos Small rotation ok, not necessary through $ 45^∘ $
– Narasimham
yesterday
add a comment |
Thanks for contributing an answer to Mathematics Stack Exchange!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Some of your past answers have not been well-received, and you're in danger of being blocked from answering.
Please pay close attention to the following guidance:
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f3055202%2fwhy-looks-the-moire-pattern-on-my-screen-like-the-contour-plot-of-z-xy%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Maybe it is because of how the phone's camera is composed.
– manooooh
Dec 28 '18 at 19:10
what type (technology) of screen is it ?
– G Cab
Dec 29 '18 at 17:48
3
xkcd.com/1814 Still cracks me up every time I read it.
– heropup
Dec 30 '18 at 5:52