How do I prove this using van-Kampen theorem informally ? (2)
$begingroup$
The second( and the last) problem is this
Could someone please help me how to calculate $pi_1(X)$?
algebraic-topology
asked Dec 17 '14 at 18:15
RubertosRubertos
5,6802824
$endgroup$
add a comment |
$begingroup$
The second( and the last) problem is this
Could someone please help me how to calculate $pi_1(X)$?
algebraic-topology
asked Dec 17 '14 at 18:15
RubertosRubertos
5,6802824
$endgroup$
$begingroup$
@DanielRust I want to believe it..
$endgroup$
– Rubertos
Dec 17 '14 at 18:22
$begingroup$
Is that a link, @Rubertos?
$endgroup$
– Balarka Sen
Dec 17 '14 at 18:37
$begingroup$
@BalarkaSen No, I can just upload a picture for you. It's just one page
$endgroup$
– Rubertos
Dec 17 '14 at 18:39
add a comment |
$begingroup$
The second( and the last) problem is this
Could someone please help me how to calculate $pi_1(X)$?
algebraic-topology
asked Dec 17 '14 at 18:15
RubertosRubertos
5,6802824
$endgroup$
The second( and the last) problem is this
Could someone please help me how to calculate $pi_1(X)$?
algebraic-topology
algebraic-topology
asked Dec 17 '14 at 18:15
RubertosRubertos
5,6802824
asked Dec 17 '14 at 18:15
RubertosRubertos
5,6802824
edited Dec 19 '15 at 1:17
Rubertos
asked Dec 17 '14 at 18:15
RubertosRubertos
5,6802824
asked Dec 17 '14 at 18:15
RubertosRubertos
5,6802824
asked Dec 17 '14 at 18:15
RubertosRubertos
5,6802824
5,6802824
$begingroup$
@DanielRust I want to believe it..
$endgroup$
– Rubertos
Dec 17 '14 at 18:22
$begingroup$
Is that a link, @Rubertos?
$endgroup$
– Balarka Sen
Dec 17 '14 at 18:37
$begingroup$
@BalarkaSen No, I can just upload a picture for you. It's just one page
$endgroup$
– Rubertos
Dec 17 '14 at 18:39
add a comment |
$begingroup$
@DanielRust I want to believe it..
$endgroup$
– Rubertos
Dec 17 '14 at 18:22
$begingroup$
Is that a link, @Rubertos?
$endgroup$
– Balarka Sen
Dec 17 '14 at 18:37
$begingroup$
@BalarkaSen No, I can just upload a picture for you. It's just one page
$endgroup$
– Rubertos
Dec 17 '14 at 18:39
$begingroup$
@DanielRust I want to believe it..
$endgroup$
– Rubertos
Dec 17 '14 at 18:22
$begingroup$
@DanielRust I want to believe it..
$endgroup$
– Rubertos
Dec 17 '14 at 18:22
$begingroup$
Is that a link, @Rubertos?
$endgroup$
– Balarka Sen
Dec 17 '14 at 18:37
$begingroup$
Is that a link, @Rubertos?
$endgroup$
– Balarka Sen
Dec 17 '14 at 18:37
$begingroup$
@BalarkaSen No, I can just upload a picture for you. It's just one page
$endgroup$
– Rubertos
Dec 17 '14 at 18:39
$begingroup$
@BalarkaSen No, I can just upload a picture for you. It's just one page
$endgroup$
– Rubertos
Dec 17 '14 at 18:39
add a comment |
2 Answers
2
active
oldest
votes
$begingroup$
An informal calculation might go as follows. First, let's "push" one of the circles to infinity so that we're instead removing a copy of $S^1$ from $mathbb{R}^3$ and a copy of $mathbb{R}$ which 'goes through' the circle and goes off towards infinity along the $z$-coordinate. You should hopefully be able to see that this space is a kind of 'maximally fattened up torus' in $3$-space. That is, if we just start expanding the torus as much as we can in all direction in $mathbb{R}^3$, the only bits which we would not be able to 'fill in' by this fattening process would be a circle inside the complement of the torus, and a line going through the 'hole' in our torus. So our space should have the same fundamental group as the torus, namely $mathbb{Z}^2$.
To prove this formally, one would need to use Van-Kampen's theorem, to show that $pi_1(S^3setminus L)cong pi_1(mathbb{R}^3setminus L)$ where we view $S^3$ as the one-point compactification of $mathbb{R}^3$. This makes the 'pushing the circle to infinity' part of the above actually work. The 'fattening up' process is really just saying that this new space deformaiton retracts onto a torus.
answered Dec 17 '14 at 18:30
Dan RustDan Rust
22.8k114884
$endgroup$
$begingroup$
(Sorry I have to leave so won't be able to answer any questions about this, admittedly hard to visualise, answer - hopefully someone else can help if it's needed)
$endgroup$
– Dan Rust
Dec 17 '14 at 18:33
$begingroup$
I get it. Thank you so much!!
$endgroup$
– Rubertos
Dec 17 '14 at 18:50
add a comment |
$begingroup$
You also need to understand the intuition of a relation at a crossing, as follows:
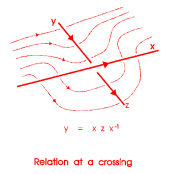
I have demonstrated this to children with a copper tubing pentoil and a nice length of rope. For the connection with the van Kampen theorem, see my book Topology and Groupoids, p. 349.
answered Dec 17 '14 at 18:55
Ronnie BrownRonnie Brown
12k12938
$endgroup$
add a comment |
Your Answer
StackExchange.ifUsing("editor", function () {
return StackExchange.using("mathjaxEditing", function () {
StackExchange.MarkdownEditor.creationCallbacks.add(function (editor, postfix) {
StackExchange.mathjaxEditing.prepareWmdForMathJax(editor, postfix, [["$", "$"], ["\\(","\\)"]]);
});
});
}, "mathjax-editing");
StackExchange.ready(function() {
var channelOptions = {
tags: "".split(" "),
id: "69"
};
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function() {
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled) {
StackExchange.using("snippets", function() {
createEditor();
});
}
else {
createEditor();
}
});
function createEditor() {
StackExchange.prepareEditor({
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader: {
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
},
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
});
}
});
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f1072289%2fhow-do-i-prove-this-using-van-kampen-theorem-informally-2%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
2 Answers
2
active
oldest
votes
2 Answers
2
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
An informal calculation might go as follows. First, let's "push" one of the circles to infinity so that we're instead removing a copy of $S^1$ from $mathbb{R}^3$ and a copy of $mathbb{R}$ which 'goes through' the circle and goes off towards infinity along the $z$-coordinate. You should hopefully be able to see that this space is a kind of 'maximally fattened up torus' in $3$-space. That is, if we just start expanding the torus as much as we can in all direction in $mathbb{R}^3$, the only bits which we would not be able to 'fill in' by this fattening process would be a circle inside the complement of the torus, and a line going through the 'hole' in our torus. So our space should have the same fundamental group as the torus, namely $mathbb{Z}^2$.
To prove this formally, one would need to use Van-Kampen's theorem, to show that $pi_1(S^3setminus L)cong pi_1(mathbb{R}^3setminus L)$ where we view $S^3$ as the one-point compactification of $mathbb{R}^3$. This makes the 'pushing the circle to infinity' part of the above actually work. The 'fattening up' process is really just saying that this new space deformaiton retracts onto a torus.
answered Dec 17 '14 at 18:30
Dan RustDan Rust
22.8k114884
$endgroup$
$begingroup$
(Sorry I have to leave so won't be able to answer any questions about this, admittedly hard to visualise, answer - hopefully someone else can help if it's needed)
$endgroup$
– Dan Rust
Dec 17 '14 at 18:33
$begingroup$
I get it. Thank you so much!!
$endgroup$
– Rubertos
Dec 17 '14 at 18:50
add a comment |
$begingroup$
An informal calculation might go as follows. First, let's "push" one of the circles to infinity so that we're instead removing a copy of $S^1$ from $mathbb{R}^3$ and a copy of $mathbb{R}$ which 'goes through' the circle and goes off towards infinity along the $z$-coordinate. You should hopefully be able to see that this space is a kind of 'maximally fattened up torus' in $3$-space. That is, if we just start expanding the torus as much as we can in all direction in $mathbb{R}^3$, the only bits which we would not be able to 'fill in' by this fattening process would be a circle inside the complement of the torus, and a line going through the 'hole' in our torus. So our space should have the same fundamental group as the torus, namely $mathbb{Z}^2$.
To prove this formally, one would need to use Van-Kampen's theorem, to show that $pi_1(S^3setminus L)cong pi_1(mathbb{R}^3setminus L)$ where we view $S^3$ as the one-point compactification of $mathbb{R}^3$. This makes the 'pushing the circle to infinity' part of the above actually work. The 'fattening up' process is really just saying that this new space deformaiton retracts onto a torus.
answered Dec 17 '14 at 18:30
Dan RustDan Rust
22.8k114884
$endgroup$
$begingroup$
(Sorry I have to leave so won't be able to answer any questions about this, admittedly hard to visualise, answer - hopefully someone else can help if it's needed)
$endgroup$
– Dan Rust
Dec 17 '14 at 18:33
$begingroup$
I get it. Thank you so much!!
$endgroup$
– Rubertos
Dec 17 '14 at 18:50
add a comment |
$begingroup$
An informal calculation might go as follows. First, let's "push" one of the circles to infinity so that we're instead removing a copy of $S^1$ from $mathbb{R}^3$ and a copy of $mathbb{R}$ which 'goes through' the circle and goes off towards infinity along the $z$-coordinate. You should hopefully be able to see that this space is a kind of 'maximally fattened up torus' in $3$-space. That is, if we just start expanding the torus as much as we can in all direction in $mathbb{R}^3$, the only bits which we would not be able to 'fill in' by this fattening process would be a circle inside the complement of the torus, and a line going through the 'hole' in our torus. So our space should have the same fundamental group as the torus, namely $mathbb{Z}^2$.
To prove this formally, one would need to use Van-Kampen's theorem, to show that $pi_1(S^3setminus L)cong pi_1(mathbb{R}^3setminus L)$ where we view $S^3$ as the one-point compactification of $mathbb{R}^3$. This makes the 'pushing the circle to infinity' part of the above actually work. The 'fattening up' process is really just saying that this new space deformaiton retracts onto a torus.
answered Dec 17 '14 at 18:30
Dan RustDan Rust
22.8k114884
$endgroup$
An informal calculation might go as follows. First, let's "push" one of the circles to infinity so that we're instead removing a copy of $S^1$ from $mathbb{R}^3$ and a copy of $mathbb{R}$ which 'goes through' the circle and goes off towards infinity along the $z$-coordinate. You should hopefully be able to see that this space is a kind of 'maximally fattened up torus' in $3$-space. That is, if we just start expanding the torus as much as we can in all direction in $mathbb{R}^3$, the only bits which we would not be able to 'fill in' by this fattening process would be a circle inside the complement of the torus, and a line going through the 'hole' in our torus. So our space should have the same fundamental group as the torus, namely $mathbb{Z}^2$.
To prove this formally, one would need to use Van-Kampen's theorem, to show that $pi_1(S^3setminus L)cong pi_1(mathbb{R}^3setminus L)$ where we view $S^3$ as the one-point compactification of $mathbb{R}^3$. This makes the 'pushing the circle to infinity' part of the above actually work. The 'fattening up' process is really just saying that this new space deformaiton retracts onto a torus.
answered Dec 17 '14 at 18:30
Dan RustDan Rust
22.8k114884
answered Dec 17 '14 at 18:30
Dan RustDan Rust
22.8k114884
answered Dec 17 '14 at 18:30
Dan RustDan Rust
22.8k114884
answered Dec 17 '14 at 18:30
Dan RustDan Rust
22.8k114884
22.8k114884
$begingroup$
(Sorry I have to leave so won't be able to answer any questions about this, admittedly hard to visualise, answer - hopefully someone else can help if it's needed)
$endgroup$
– Dan Rust
Dec 17 '14 at 18:33
$begingroup$
I get it. Thank you so much!!
$endgroup$
– Rubertos
Dec 17 '14 at 18:50
add a comment |
$begingroup$
(Sorry I have to leave so won't be able to answer any questions about this, admittedly hard to visualise, answer - hopefully someone else can help if it's needed)
$endgroup$
– Dan Rust
Dec 17 '14 at 18:33
$begingroup$
I get it. Thank you so much!!
$endgroup$
– Rubertos
Dec 17 '14 at 18:50
$begingroup$
(Sorry I have to leave so won't be able to answer any questions about this, admittedly hard to visualise, answer - hopefully someone else can help if it's needed)
$endgroup$
– Dan Rust
Dec 17 '14 at 18:33
$begingroup$
(Sorry I have to leave so won't be able to answer any questions about this, admittedly hard to visualise, answer - hopefully someone else can help if it's needed)
$endgroup$
– Dan Rust
Dec 17 '14 at 18:33
$begingroup$
I get it. Thank you so much!!
$endgroup$
– Rubertos
Dec 17 '14 at 18:50
$begingroup$
I get it. Thank you so much!!
$endgroup$
– Rubertos
Dec 17 '14 at 18:50
add a comment |
$begingroup$
You also need to understand the intuition of a relation at a crossing, as follows:
I have demonstrated this to children with a copper tubing pentoil and a nice length of rope. For the connection with the van Kampen theorem, see my book Topology and Groupoids, p. 349.
answered Dec 17 '14 at 18:55
Ronnie BrownRonnie Brown
12k12938
$endgroup$
add a comment |
$begingroup$
You also need to understand the intuition of a relation at a crossing, as follows:
I have demonstrated this to children with a copper tubing pentoil and a nice length of rope. For the connection with the van Kampen theorem, see my book Topology and Groupoids, p. 349.
answered Dec 17 '14 at 18:55
Ronnie BrownRonnie Brown
12k12938
$endgroup$
add a comment |
$begingroup$
You also need to understand the intuition of a relation at a crossing, as follows:
I have demonstrated this to children with a copper tubing pentoil and a nice length of rope. For the connection with the van Kampen theorem, see my book Topology and Groupoids, p. 349.
answered Dec 17 '14 at 18:55
Ronnie BrownRonnie Brown
12k12938
$endgroup$
You also need to understand the intuition of a relation at a crossing, as follows:
I have demonstrated this to children with a copper tubing pentoil and a nice length of rope. For the connection with the van Kampen theorem, see my book Topology and Groupoids, p. 349.
answered Dec 17 '14 at 18:55
Ronnie BrownRonnie Brown
12k12938
edited Jan 14 at 15:06
answered Dec 17 '14 at 18:55
Ronnie BrownRonnie Brown
12k12938
answered Dec 17 '14 at 18:55
Ronnie BrownRonnie Brown
12k12938
answered Dec 17 '14 at 18:55
Ronnie BrownRonnie Brown
12k12938
12k12938
add a comment |
add a comment |
Thanks for contributing an answer to Mathematics Stack Exchange!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f1072289%2fhow-do-i-prove-this-using-van-kampen-theorem-informally-2%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
$begingroup$
@DanielRust I want to believe it..
$endgroup$
– Rubertos
Dec 17 '14 at 18:22
$begingroup$
Is that a link, @Rubertos?
$endgroup$
– Balarka Sen
Dec 17 '14 at 18:37
$begingroup$
@BalarkaSen No, I can just upload a picture for you. It's just one page
$endgroup$
– Rubertos
Dec 17 '14 at 18:39